弾性構造物の設計で一番よく使われるのが応力解析で、その次が固有値解析です。できれば応力解析用の要素分割が出来た時点で固有値解析をし、予想通りの固有振動周波数がでるかどうかを確認すべきです。その周波数が出ないとなると要素分割が悪いかまたは解析用のソフトが悪いかのどちらかになります。購入した実験機器がおもわしくない結果を出す時があります。それは多分、機器のファインチューニングを怠ったためです。数値解析も同じようにソフトと要素分割のファインチューニングが必要です。ちょっとしたことにも目をくばることにより、より信頼性の高い解析結果を得ることができ、また良い製品設計ができることになります。つまり、固有値解析は全ての解析の入口であると私は考えます。 ここでは、3次元弾性構造物の固有値解析とソフト開発について述べますが、その前に計算結果の検証のために、厳密解が存在する1次元のビームの運動方程式の話をし、幾つかのケースについて固有値を計算してみます。その後、3次元の運動方程式とソフトの作り方を説明します。最後に、ビームを3次元ソフトで固有値計算をし、1次元の厳密解に近いかどうかをチェックします。
■梁の運動方程式と固有値■
数値計算による3次元弾性体の固有振動周波数または固有値の計算精度を調べるために、よく梁が使われます。ここでもE、I、ρが一定の梁を使って3次元弾性体の固有値の計算精度を調べることにします。そのためには、なにかReferenceになるものが必要です。ここでは、1次元の梁の運動方程式を導き固有値を計算し、それをReferenceにします。そのためには、Newtonの第2の法則であるΣFv=mavを導かねばなりません。添え字のvはvertical(天地方向)のことです。ここでは、式の導出と計算例を載せてあります。例題の計算では、片持ち梁と両端フリーの梁の固有振動数を取り上げました。
ビームでは1次元の微分方程式を用いて変位や応力を計算しています。次元を落とすと、欠落する次元をカバーするために新しい変数を導入しなければなりません。ビームでは、長手方向(x軸)に対し荷重方向の変位のみが残りますので、せん断応力(τxy)によるビームの変形をせん断力Vyで、断面での法線応力(τxx)を断面形状(Zz)と合わせてモーメントMzで表します。つまり、τxx=Mz/Zzその他の変位や応力は全てゼロとしています。まず、3次元の弾性応力解析ではどのような式からスタートしたかをみて見ましょう。下式を見て下さい。
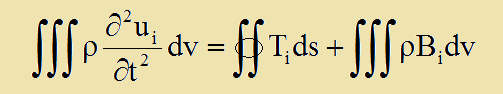
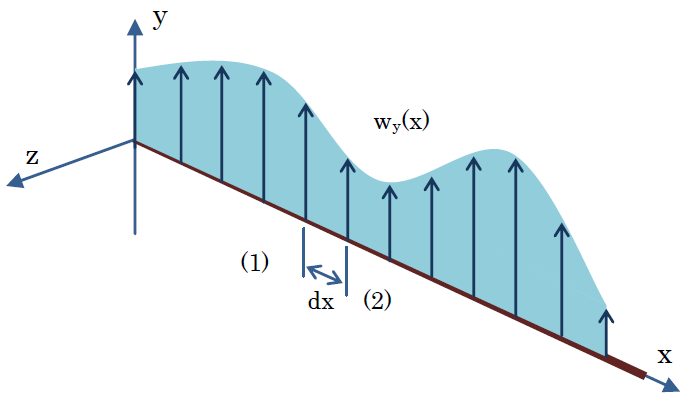
ここに、ρ=固体密度(Density)[Kg/m3]、ui=変位(Displacement)[m]、Ti=表面外力(Surface Traction)[Pa]、ρBi=内部外力(Body Force)[N/m3]を意味します。 下図は、1次元ビームに分布荷重wy(x) [N/m]が掛けられている状態を示しています。ビームの中立軸が座標xで荷重方向の座標がyです。座標zは、手前に向いています。つまり、ここでは座標yが重力加速度方向です。
| Sound Eigen | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |