■FEMでの微分の計算■
ここでは、最も簡単で精度の良い関数の1階微分の数値計算方法を紹介します。
差分法では、微分の計算方法が、解析の全てを支配していますが、有限要素法のプログラムで数値微分(差分)を行うことは、めったにありません。皆無といっていいでしょう。かといって、有限要素法において、微分の計算がないわけではありません。実をいうと、FEMのプログラムは、微分と積分のかたまりのようなものです。しかし、微分の計算の殆どは、マトリックス演算の中に隠れています。ただ、プログラムの中で、目で確認できる微分といえば、形状関数の導関数です。

市販のプログラムでは、あらかじめ手で形状関数(Shape Function)の導関数を求めておいて、プログラムの中で、微分を導関数から求めます。
例えば、形状関数が、f(x)=x² である場合、導関数は、f'(x)=2x になります。つまり、x=0.5 でのf(x)の微分値は、1 になります。
しかし、この場合、形状関数は、FEMで最重要品目ですから、導関数を求める手計算に間違いがあると、プログラム中の全てのプロセスに影響します。つまり、間違った結果を出力することになります。

このサイトで紹介しているFEMプログラムでは、形状関数(Shape Function)の導関数を導いていません。その代わりに、差分により微分を数値的に計算します。この方法だと導関数を準備しておく必要がないので、上の様な間違いを防ぐことが出来ます。もちろん、微分の計算誤差には、細心の注意を払う必要があります。

■2次式の微分■
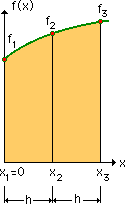
では、どのようにすれば、微分が計算できるか考えてみましょう。下の左図を見て下さい。図の曲線上の3点を通過させるためには、f(x)を最低2次式にする必要がある。下の右図がその式になります。

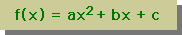定数 c は、x₁=0 でのf(x)の値であるから、c=f₁となります。